1   問(wèn)題的提出

隨著全站儀在工程測(cè)量中應(yīng)用的逐漸普及,采用導(dǎo)線(xiàn)作為測(cè)量的平面控制越來(lái)越廣泛，導(dǎo)線(xiàn)一般多布設(shè)成單一導(dǎo)線(xiàn)。應(yīng)用全站儀觀測(cè)導(dǎo)線(xiàn)，可以通過(guò)機(jī)內(nèi)的微處理器，直接得到地面點(diǎn)的平面近似坐標(biāo)，因此在成果處理時(shí)可以應(yīng)用這些近似坐標(biāo)直接按坐標(biāo)平差（即間接平差）法進(jìn)行平差。這將優(yōu)于過(guò)去導(dǎo)線(xiàn)計(jì)算過(guò)程中先進(jìn)行邊、角平差后，再求取坐標(biāo)的方法。本文主要針對(duì)采用全站儀觀測(cè)導(dǎo)線(xiàn)的近似平差和嚴(yán)密平差方法進(jìn)行探討。

2   導(dǎo)線(xiàn)的近似坐標(biāo)平差

　　導(dǎo)線(xiàn)測(cè)量用于圖根控制等低精度測(cè)量中，往往采用近似平差即可。由于全站儀直接測(cè)定各導(dǎo)線(xiàn)點(diǎn)的近似坐標(biāo)值，平差計(jì)算就不用像傳統(tǒng)的導(dǎo)線(xiàn)近似平差計(jì)算那樣，先進(jìn)行角度閉合差計(jì)算和調(diào)整，然后推算方位角，再進(jìn)行坐標(biāo)增量閉合差的計(jì)算和調(diào)整，最后根據(jù)平差后的坐標(biāo)增量計(jì)算導(dǎo)線(xiàn)點(diǎn)的坐標(biāo)。全站儀觀測(cè)導(dǎo)線(xiàn)直接按坐標(biāo)平差計(jì)算，將更為簡(jiǎn)便。直接按坐標(biāo)平差法計(jì)算步驟如下：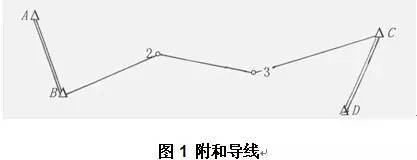

采用坐標(biāo)法進(jìn)行導(dǎo)線(xiàn)近似平差，直接在已經(jīng)測(cè)得導(dǎo)線(xiàn)點(diǎn)的坐標(biāo)上進(jìn)行改正，方法簡(jiǎn)單，易于掌握，避免了傳統(tǒng)近似平差法的方位角的推算和改正，以及坐標(biāo)增量的計(jì)算和改正，能大大提高工作效率，而且不易出錯(cuò)。同時(shí)可以看出傳統(tǒng)附和導(dǎo)線(xiàn)測(cè)量需要兩條已知邊，作為方位角的檢核條件，而直接坐標(biāo)法，只需要一條已知邊和一個(gè)已知點(diǎn)即可，使導(dǎo)線(xiàn)的布網(wǎng)更加靈活。

3   導(dǎo)線(xiàn)的嚴(yán)密坐標(biāo)平差

高等級(jí)平面控制測(cè)量對(duì)精度的要求較高，需要嚴(yán)密平差。全站儀觀測(cè)的導(dǎo)線(xiàn)采用嚴(yán)密坐標(biāo)平差法較為適宜。嚴(yán)密坐標(biāo)平差取待定點(diǎn)的坐標(biāo)平差值作為未知數(shù)，通過(guò)平差計(jì)算可直接得到各待定點(diǎn)的坐標(biāo)。但過(guò)去影響應(yīng)用坐標(biāo)平差（間接平差）法的主要原因是輔助計(jì)算量大，尤其是在列立誤差方程之前,需要按近似平差方法將全部導(dǎo)線(xiàn)點(diǎn)的近似坐標(biāo)推算出來(lái)；采用全站儀觀測(cè)導(dǎo)線(xiàn)，在測(cè)量中可直接得到待定點(diǎn)的近似坐標(biāo)，因此不必再解算待定點(diǎn)的近似坐標(biāo)。另一方面坐標(biāo)平差法誤差方程式的列立簡(jiǎn)單且有規(guī)律性，便于編制程序。坐標(biāo)平差法雖然法方程的階數(shù)較高，但利用編制的程序輸入計(jì)算機(jī)中解算，仍是快捷迅速的，這是傳統(tǒng)條件平差無(wú)可比擬的，因此采用坐標(biāo)平差法平差全站儀導(dǎo)線(xiàn)是比較適宜的。

3.1   坐標(biāo)平差中邊、角觀測(cè)值權(quán)的確定

　　坐標(biāo)平差已是一種成型的平差方法，有關(guān)其原理、計(jì)算公式和計(jì)算步驟等在各種平差文獻(xiàn)中都有較細(xì)的推導(dǎo)和敘述，這里只就應(yīng)用該法平差全站儀觀測(cè)導(dǎo)線(xiàn)過(guò)程中，有關(guān)邊、角權(quán)的確定方法談一點(diǎn)體會(huì)。

3.1.1   邊、角觀測(cè)誤差方程式

　　坐標(biāo)平差法計(jì)算，首先是列立誤差方程式。導(dǎo)線(xiàn)平差有角度和邊長(zhǎng)兩種類(lèi)型誤差方程式，在圖2中，β為觀測(cè)角度，略去推導(dǎo)過(guò)程，其誤差方程為：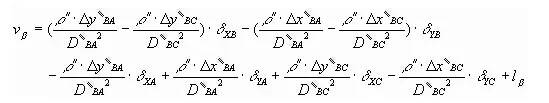

應(yīng)用上述兩類(lèi)誤差方程式組成法方程式時(shí)，因邊、角的觀測(cè)精度不等，則其權(quán)不等。即使邊之間或角度之間若非等精度觀測(cè)，其權(quán)數(shù)也是不等的。因此就要合理地確定其權(quán)數(shù)，觀測(cè)值的權(quán)是組成法方程的重要元素，權(quán)確定的合理與否，直接影響到計(jì)算結(jié)果。

3.1.2   單位權(quán)中誤差和權(quán)的確定

　　應(yīng)用全站儀觀測(cè)的導(dǎo)線(xiàn)，測(cè)距精度較高，通常邊、角同時(shí)測(cè)得，據(jù)此筆者認(rèn)為按如下方法確定其權(quán)較為合理。

(1)導(dǎo)線(xiàn)所有的轉(zhuǎn)折角因測(cè)量的測(cè)回?cái)?shù)相等，按等權(quán)對(duì)待，并設(shè)角度觀測(cè)中誤差為單位權(quán)中誤差，即μ0=mβ。

(2)導(dǎo)線(xiàn)邊的觀測(cè)，因各邊距離不等，則各邊的距離觀測(cè)精度不等，可以根據(jù)全站儀的標(biāo)稱(chēng)測(cè)距精度求出每條邊的測(cè)距中誤差，再按權(quán)的定義公式 ，確定每一條邊的權(quán)值。

　　例如：用拓普康GTS-701全站儀觀測(cè)了一條導(dǎo)線(xiàn)，現(xiàn)就其單位權(quán)中誤差的確定方法和權(quán)的計(jì)算方法加以說(shuō)明：

　　該儀器的測(cè)角標(biāo)稱(chēng)精度為±2″，若對(duì)導(dǎo)線(xiàn)所有轉(zhuǎn)折角進(jìn)行一測(cè)回觀測(cè)，則角度的觀測(cè)中誤差mβ=±2″，距離觀測(cè)標(biāo)稱(chēng)精度為±（3+2×10-6·D）mm，其中D為觀測(cè)邊的距離，以公里為單位。

　　因此可以根據(jù)觀測(cè)邊的距離計(jì)算出每條邊的中誤差。例如某條邊的觀測(cè)距離為1325.375m，則該邊的距離觀測(cè)中誤差為mD為

mD=±(3+2×1.325375)mm=±5.65mm。

　　權(quán)的確定可取角度觀測(cè)中誤差為單位權(quán)中誤差，即μ0=mβ=2″，則角度觀測(cè)值的權(quán)Pβ為：

4   結(jié)語(yǔ)

　　綜上所述，在導(dǎo)線(xiàn)平面控制測(cè)量中，應(yīng)用全站儀觀測(cè)，因?yàn)榇c(diǎn)的近似坐標(biāo)在觀測(cè)時(shí)可同時(shí)得到。針對(duì)該情況，在此分別提出了近似和嚴(yán)密的坐標(biāo)平差方法，供讀者在實(shí)際應(yīng)用中參考。一般低等級(jí)控制測(cè)量采用近似坐標(biāo)平差就可滿(mǎn)足精度要求，高等級(jí)控制測(cè)量應(yīng)采用嚴(yán)密平差的方法進(jìn)行解算，可根據(jù)平面控制測(cè)量設(shè)計(jì)的等級(jí)和精度要求而選用相應(yīng)的平差方法。